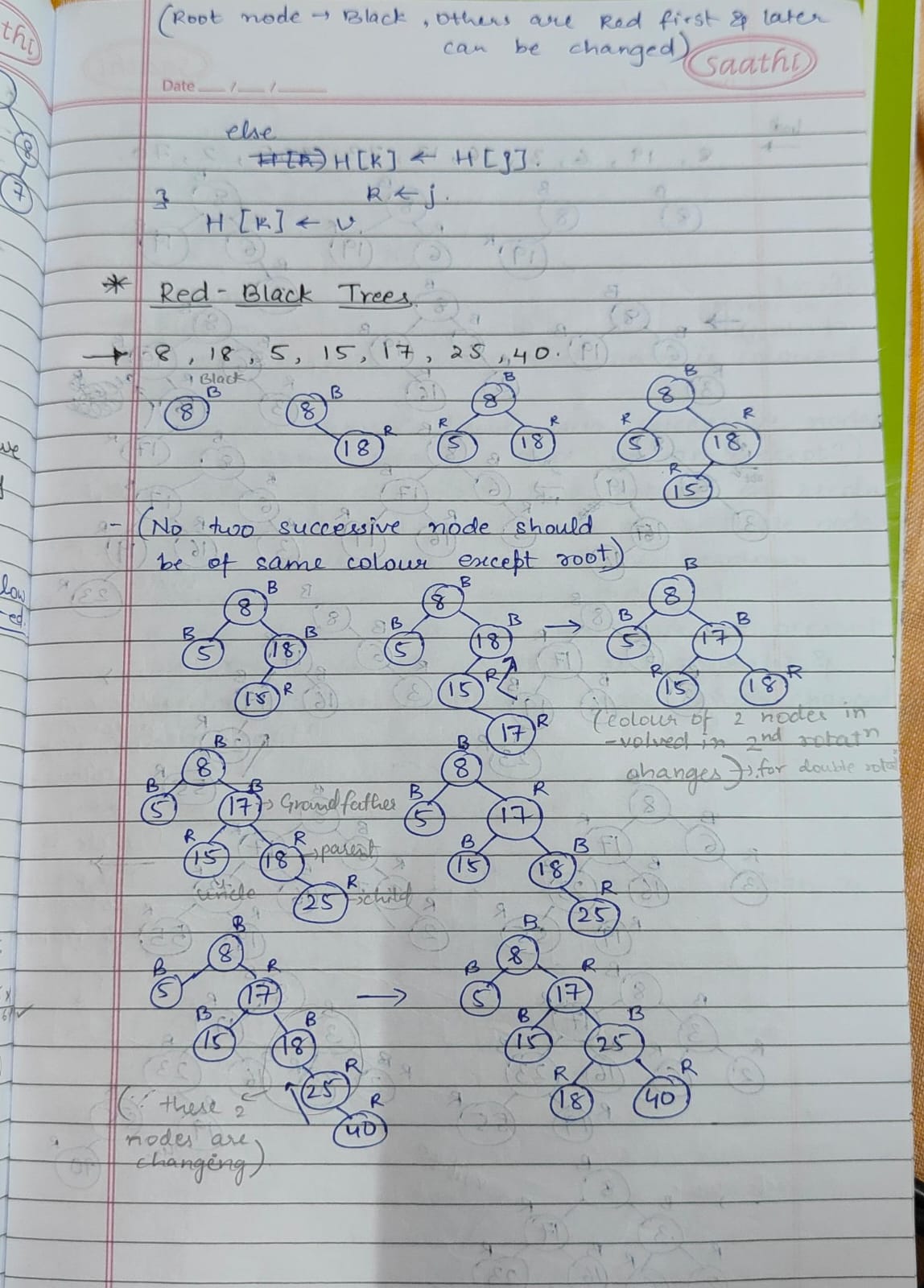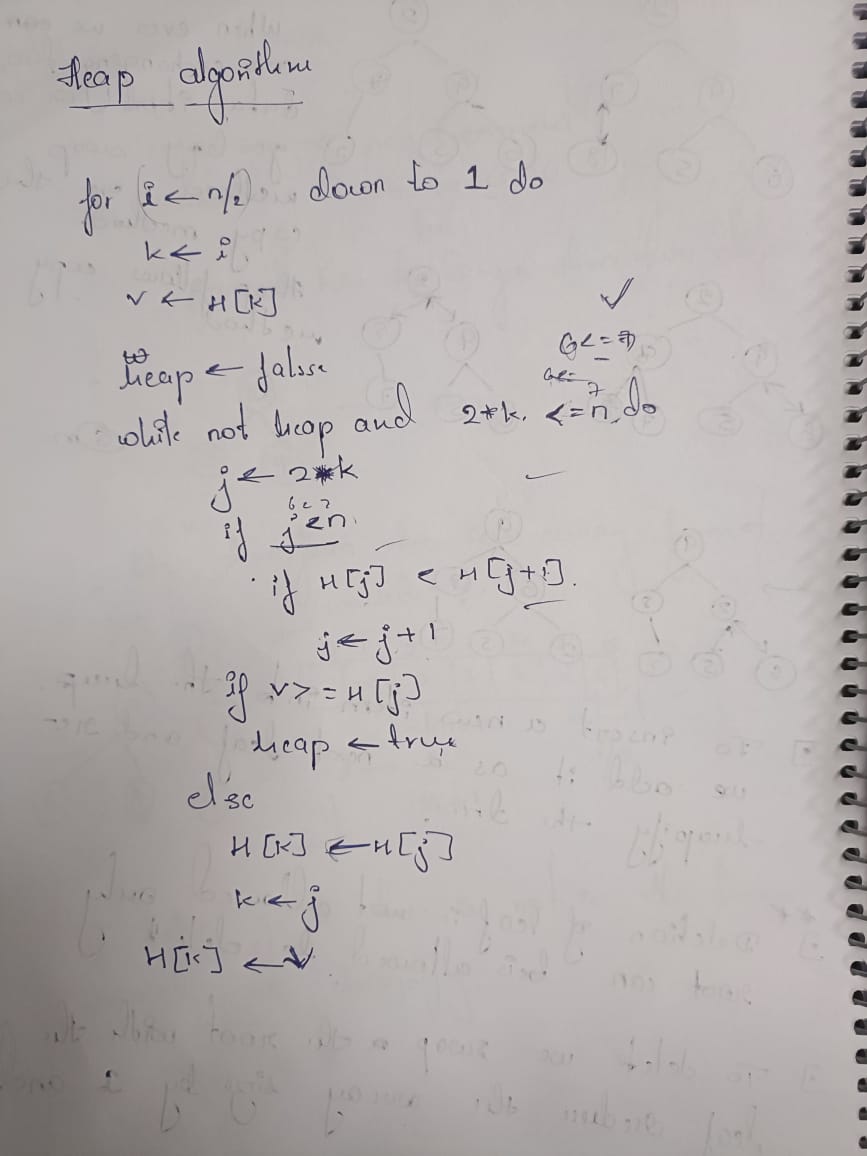Learnings from the Course

Hierarchical Data Structures:

Trees are structured to organize data through parent-child relationships. Binary Search Trees (BST) enable efficient searches, but balancing is essential, achieved through AVL or Red-Black trees. Heaps prioritize task management effectively, while Tries are ideal for operations like prefix matching in auto-complete systems. Each tree type specializes in optimizing specific tasks, making them indispensable across various applications.

Efficient Array Query Algorithms:

Advanced algorithms for array queries tackle problems such as calculating range sums or finding maximum values with remarkable efficiency. Data structures like Segment Trees and Fenwick Trees perform these operations in logarithmic time, making them invaluable in handling large datasets. These techniques find applications in fields like data analytics, competitive programming, and systems requiring real-time calculations.

Comparison of Trees and Graphs:

Trees, being hierarchical and acyclic, are used for organizing structured data such as file systems. Graphs, with their flexible and complex interconnections, are suited for modeling networks and pathways. Tree traversal methods (Inorder, Preorder) are tailored for hierarchical processing, whereas graph traversal techniques (BFS, DFS) excel in exploring connectivity and discovering optimal paths.

Network Optimization Algorithms:

Algorithms for spanning trees, like Kruskal’s, focus on minimizing costs in network infrastructure design. Shortest path algorithms, such as Dijkstra’s, are fundamental in applications like navigation and logistics. These algorithms play a critical role in optimizing connectivity and route planning for real-world networks, improving overall efficiency.

Principles of Algorithm Design and Analysis

• Decomposition: Dividing a complex problem into smaller, more manageable components, making it easier to analyze and solve.
• Pattern Recognition: Detecting repetitive patterns or structures in data or processes to create reusable solutions.
• Abstraction: Highlighting key details while omitting irrelevant complexities to simplify problem-solving.
• Lazy Propagation/Evaluation: Postponing computations until absolutely necessary, often used in optimization techniques like segment trees.
• Sliding Window: A method to efficiently handle problems involving subarrays or substrings, reducing space and time usage.
• Pruning: Cutting down unnecessary calculations or paths in a search space to enhance performance, as seen in branch-and-bound strategies.
• Memoization and Pre-computation:
  • Memoization: Saving intermediate results during execution to prevent redundant calculations.
  • Pre-computation: Preparing and storing results in advance for static datasets to improve runtime efficiency.